Golden Ratio 1 1 2 3 5

The golden ratio in nature next page by lettie mcguire.

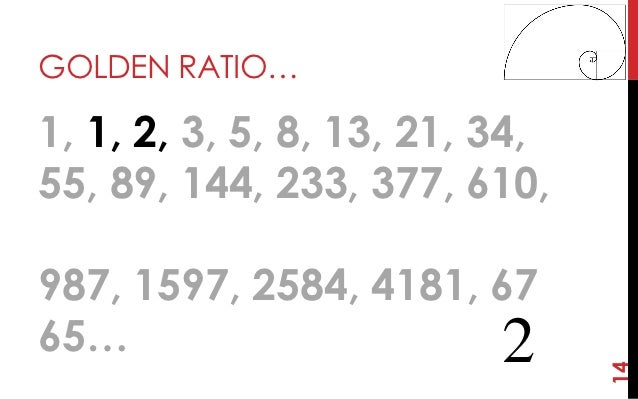
Golden ratio 1 1 2 3 5. Nature the golden ratio and fibonacci too. This is an easy way to calculate it when you need it. The goal of this lesson is to introduce the mathematical concept of the golden ratio to middle and high school age students. The golden ratio is sometimes called the divine proportion because of its frequency in the natural.

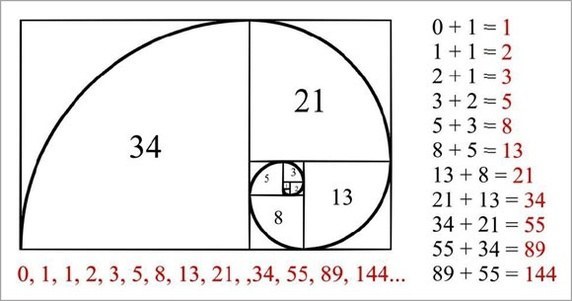
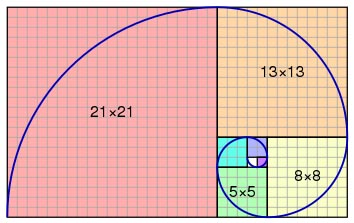
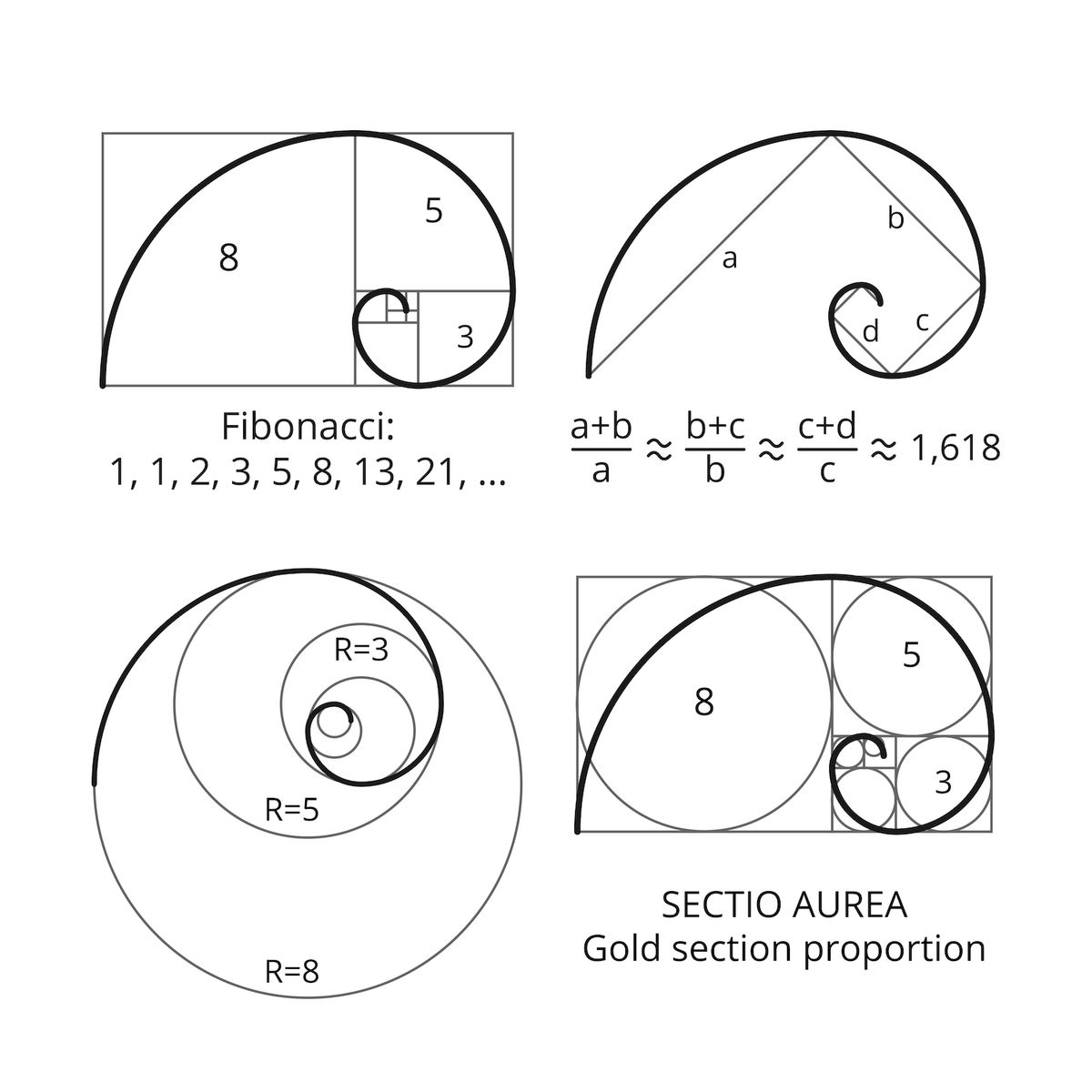
1 1 2 3 5 8 13 21. Plants can grow new cells in spirals. 1 1 2 3 5 8 13 21 34 55 89 144 233 377. The figure on the right illustrates the geometric relationship.

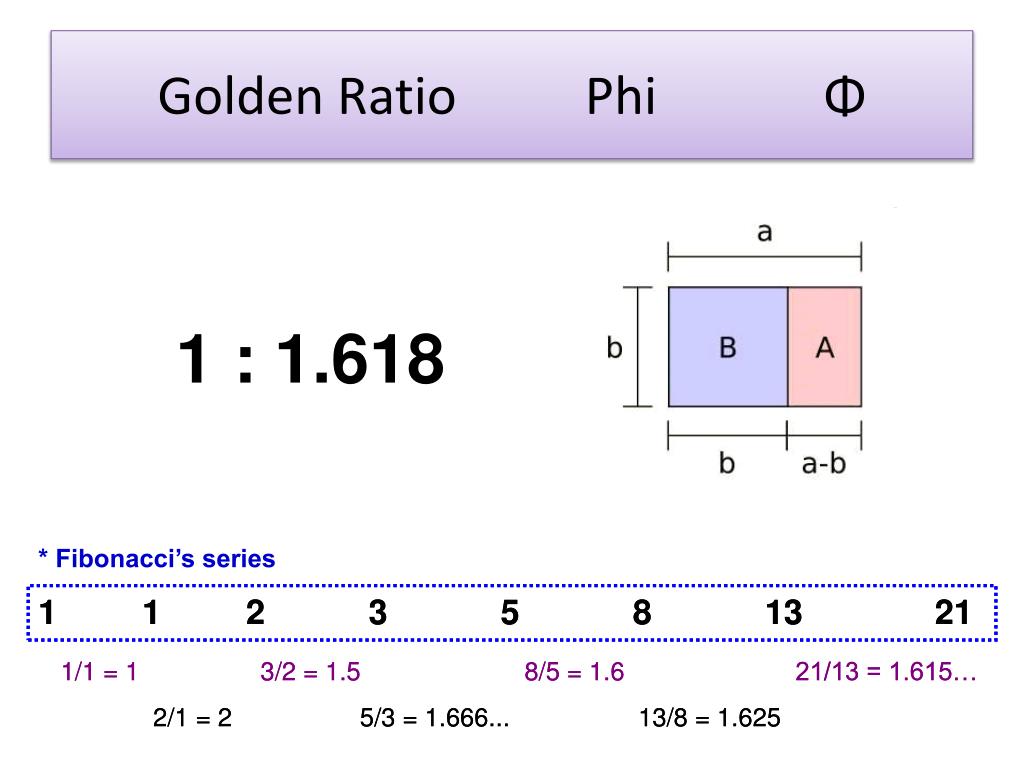
When we take any two successive one after the other fibonacci numbers their ratio is very close to the golden ratio. In mathematics two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Key takeaways the golden ratio describes predictable patterns on everything from atoms to. The value of the golden ratio which is the limit of the ratio of consecutive fibonacci numbers has a value of approximately 1 618.

The golden ratio is also equal to 2 sin 54 get your calculator and check. The golden ratio can be illustrated within special dimensions of sprials triangles and rectangles where the ratio of the length of the short side to the long side is 618 was noted by ancient greek. In fact the higher the fibonacci numbers the closer their relationship is to 1 618. Golden ratio convergence the ratio of two sequential fibonacci numbers converges to the golden ratio.

φ is the golden ratio 1 5 2 1 61803399. 2 1 1 3 2 1 5 3 2 the ratios of sequential fibonacci numbers 2 1 3 2 5 3 etc approach the golden ratio. 2 1 2 3 2 1 5 5 3 1 66666666. Introductory information about the golden ratio.

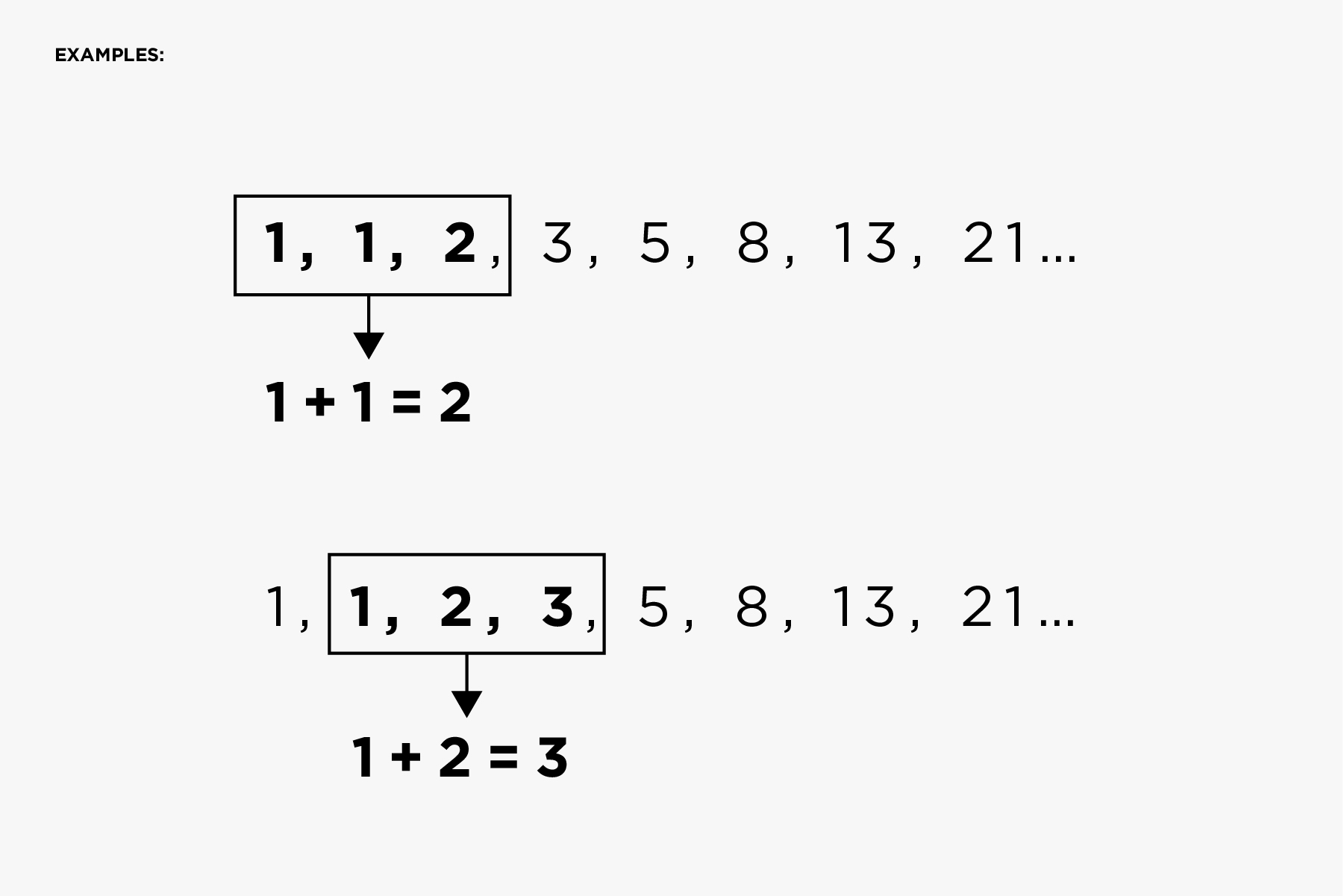
About the golden ratio. Etc each number is the sum of the two numbers before it. In the sequence each number is simply the sum of the two preceding numbers 1 1 2 3 5 8 13 etc.